Skip to main content

🟢 Chain of Thought Prompting

Chain of Thought (CoT) prompting1 is a recently developed prompting method, which encourages the LLM to explain its reasoning. The below image1 shows a few shot standard prompt (left) compared to a chain of thought prompt (right).

Regular Prompting vs CoT (Wei et al.)

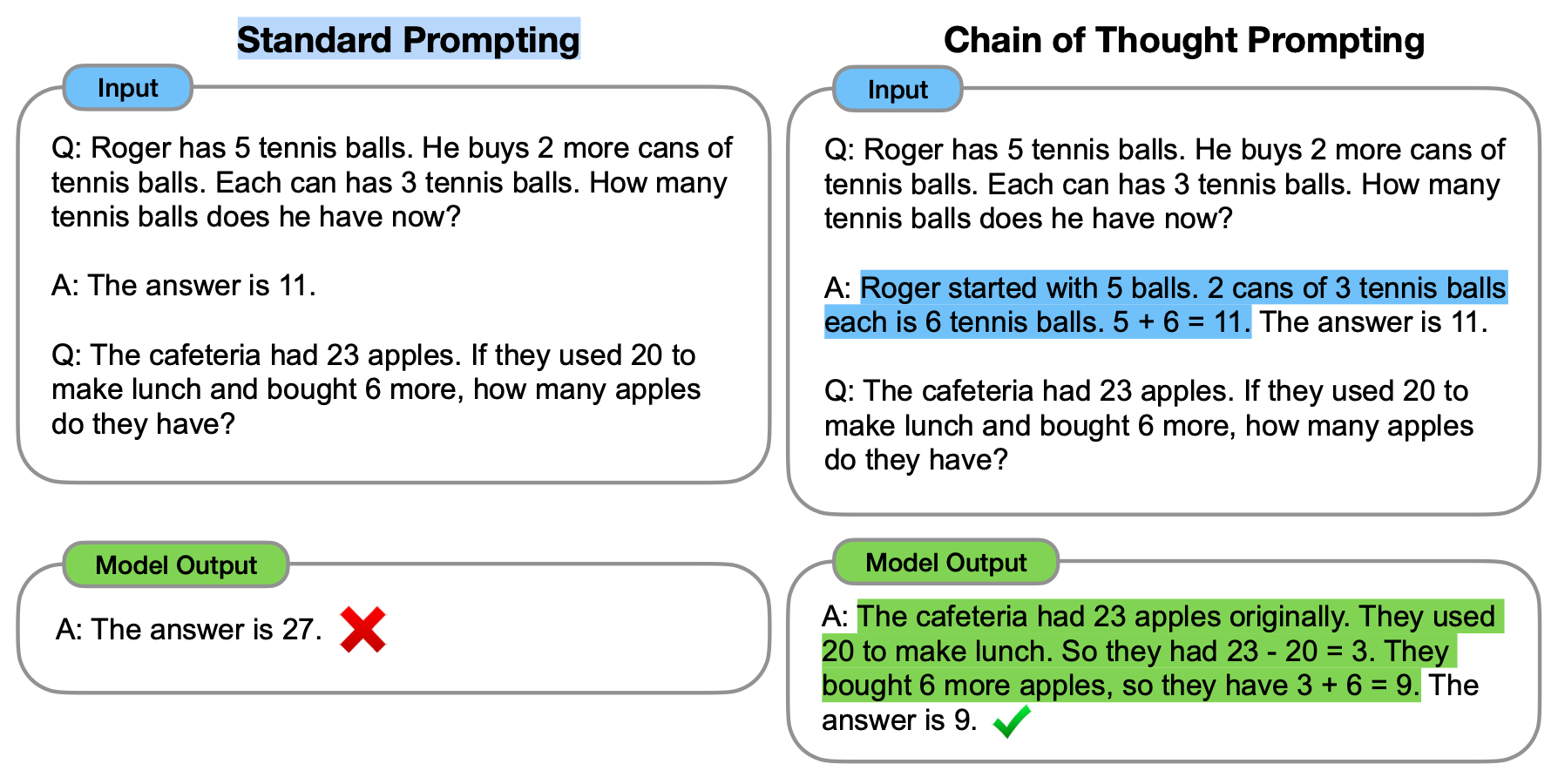
The main idea of CoT is that by showing the LLM some few shot exemplars where the reasoning process is explained in the exemplars, the LLM will also show the reasoning process when answering the prompt. This explanation of reasoning often leads to more accurate results.

Example​

Here are a few demos. The first shows GPT-3 (davinci-003) failing to solve a simple word problem. The second shows GPT-3 (davinci-003) succesfully solving the same problem, by using CoT prompting.

Incorrect​

Correct​

Results​

CoT has been shown to be effective in improving results on tasks like arithmetic, commonsense, and symbolic reasoning tasks1. In particular, prompted PaLM 540B2 achieves 57% solve rate accuracy on GSM8K3 (SOTA at the time).

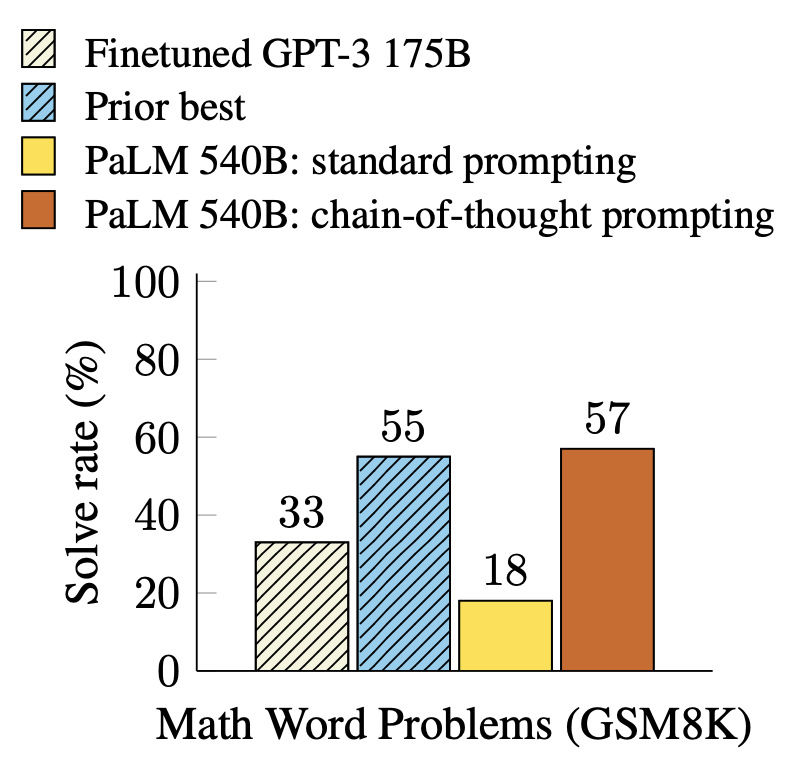
Comparison of models on the GSM8K benchmark (Wei et al.)

Limitations​

Importantly, according to Wei et al., "CoT only yields performance gains when used with models of ∼100B parameters". Smaller models wrote illogical chains of thought, which led to worse accuracy than standard prompting. Models usually get performance boosts from CoT prompting in a manner proportional to the size of the model.

Notes​

No language models were hurt finetuned in the process of writing this chapter 😊.

  1. Wei, J., Wang, X., Schuurmans, D., Bosma, M., Ichter, B., Xia, F., Chi, E., Le, Q., & Zhou, D. (2022). Chain of Thought Prompting Elicits Reasoning in Large Language Models. ↩
  2. Chowdhery, A., Narang, S., Devlin, J., Bosma, M., Mishra, G., Roberts, A., Barham, P., Chung, H. W., Sutton, C., Gehrmann, S., Schuh, P., Shi, K., Tsvyashchenko, S., Maynez, J., Rao, A., Barnes, P., Tay, Y., Shazeer, N., Prabhakaran, V., … Fiedel, N. (2022). PaLM: Scaling Language Modeling with Pathways. ↩
  3. Cobbe, K., Kosaraju, V., Bavarian, M., Chen, M., Jun, H., Kaiser, L., Plappert, M., Tworek, J., Hilton, J., Nakano, R., Hesse, C., & Schulman, J. (2021). Training Verifiers to Solve Math Word Problems. ↩